LIDIA VAZQUEZ

Fireworks Problem
Problem Statement:
The problem that has been presented in class is on the topic of quadratics. The problem is that a high school, is celebrating an athletic triumph, by having a firework display, the fireworks will be launched by the top of the school building which height is 160Ft. And will be launched at a 65 degree angle. What we are trying to figure out is the spectators safety and the timing. And the skeleton of the problem is if we strip away the story and focus on the physics and math portion. The question is if we have a parabola, with certain qualities how will we be able to calculate the x-intercepts, and the vertex. Which I will dive more in depth later. To sumarize the main idea is that we need to keep the spectators safe, so we need to know
-
What's the distance between the building and it's landing place?
-
When will the firework reach it's peak?

Work:
Before tackling the Fireworks problem again we learned several things that would be useful as tool such as.
PROCESS & SOLUTION:
Beginning:
Once I had somewhat of an understanding of the problem at hand my teammates and I began to tackle it by creating an illustration to make sense of all the information. The fireworks problem was presented to us early in the semester, to be completely honest before learning anything of parabolas, I thought that solving this problem was , not impossible but certainly very difficult especially with the few information that was provided.
These two pictures are comparing of the first time we were presented with the firework problem and the second time. The first time we had an idea of what was going on but the second drawing provides more information and were even more aware of how the shape of the parabola looks like. I visualise it like in humanities when you are brainstorming and you get out the general themes, you basically get your ideas and questions on paper, then you go in and bringing structuring your essay adding detail, defining it. That's what we did here in math, but in a cooler way.
My process and a swirl of contributions from my groupmates:
If I would explain just my process it would make no sense it would be like a blank mad libs, I solved this problem with my group the entire way through, or at least with several classmates so that's how I will explain my process.
The first day we were represented with the fireworks problem my group and I splitted the work so that we could get as much done in the white board. Brianna redrew the problem, I and steven worked and diana worked on solving for the vertex and the x-intercepts.
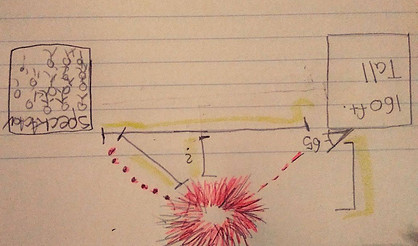
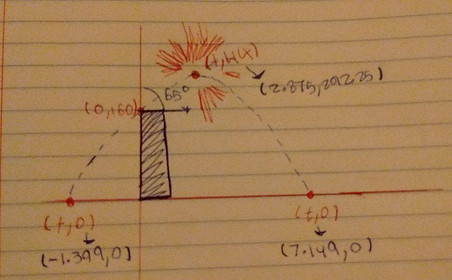
Firstly why do we need to solve for the vertex and the x-intercepts? Well as I spoke of earlier we have to get to the skeleton of the problem, which is a parabola and we discovered that we were dealing with a parabola here, because not only did we specifically work on parabolas for a long time but also, as you can see in our drawing the design of the fireworks being launched, and landing forms a shape of a parabola. So that was a huge hint, also we were trying to find were the fireworks ended for the spectators safety. That can be interpreted as one of the x-intercepts in a parabola we also wanted to calculate its highest point. In a parabola the highest or lowest point, that is also in the middle of the two intercepts, is the vertex. So there you go.
Going back to us solving this second time we were presented withh(t)=160+92t-16t2Which is very similar to f(x)=ax^2-bx+c, So steven and I proposed that it was already put in standard form so we could find the x-intercepts, We decide to try to convert it into factored form, or solve it using the Quadratic formula. So what we did is he worked on trying to factor it , and I worked on plugging it in and solving for the formula. I had a lot of failed attempts, because mathematics is beautifully exact and precise, so if I accidentally change a little thing, it can be drastically incorrect. The first day I tried and failed and tried again the method was correct I would just change the numbers or put some numbers that weren’t the correct ones because, I am human we make mistakes. But thanks to my group mates they were able to take my concept and correct my errors, and we were able to get two x- intercepts.
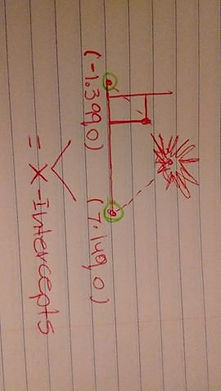
Now going back to our drawing we can add some information to it we have the two x-intercepts, so were it begins and where it ends.
Afterwards, focused on the vertex. I presented with ,my group the idea of changing our standard form into vertex form. We began working on that, Mr. Carter kindly redirected us and explained how that couldn’t work for this specific problem. The only problem was I just knew that way of finding the vertex because it was the one that I had worked on comprehending more.
Mr. Carter also very kindly proposed to us the idea of how the vertex is found in the middle of the two x-Intercepts, which we already knew what they were. Brianna Diana and I were still having difficulty coming up with the way of finding the solution.
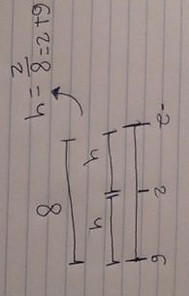
What he did in this picture is he simplified it to two points -2, and 6 those are your
two x-intercepts then well what is the middle of that? 2, then what is the
equal amount of points from -2 to 2, 4 and same with 2, and 6. And those two fours put together are 8 .
So we can use that same concept for our problem. Brianna Dianna and I did the same thing with our to find where the x axis of our vertex
After that Regina and I were unsure of how to find the solution for the y axis of the vertex. What I tried out was instead of subtracting the bigger number to find the difference we subtract the other number but that wouldn't make sense because the result would be a negative number and we can’t have a negative because the floor= the x axis of our graph we could only have a negative number if there was a hole for some reason on the ground. Which was not the case.Anyway we went back to our paper and saw this d(t)=92ttan65, well we knew the what time was so we could just plug it in.
SaoSo at the end we are given were it ends and what certain distance it goes swell as the time it takes. Also the vertex so the highest it goes. This is the final picture.
Problem Evaluation
To be completly honest, I have never liked word problems. But I really liked this problem, I believe it was because firstly we worked with everyone. And Secondly because It was presented to us at an early stage and then represented to us, this was really helpful because when we were learning about Parabolas and x-intercepts and so forth , we knew why it was useful an how we could apply it to a real situation. Also doing it in this format also was very helpful for me personally because if I didn’t understand something in the math part I could visualize it and understand why such thing was done. I would love to do more word problems like this maybe one calculating the sprinklers. Or maybe one of parabolas, like that show in Disney land world of color. We could design different parabolas and design them to do a display and also calculate so that they don’t wet the spectator.
Self Evaluation:
If I could grade myself on the quadratics unit I would give myself an A because apart from learning and doing my work, I am really proud of all my classmates that I helped and explained different parts of the problems. It really helped me understand the unit better.
Edits
Iza: The feedback she gave me was to add my self reflection and project reflection, due to the fact that I had forgotten that piece.
Estella: The feedback she gave me was that it was a little bit confusing because before I didn't provide that many visuals, and I hadn't labeled them.
I took there feedback and added visuals with titles and explanations, as well as my self reflection, and project reflection.
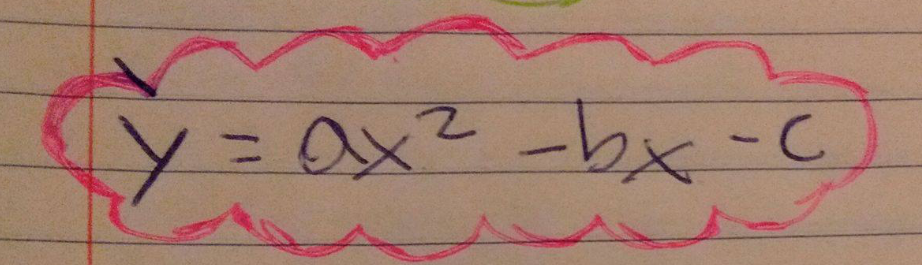
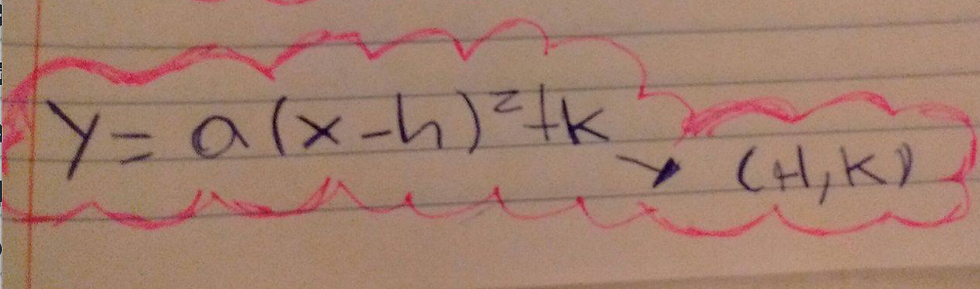
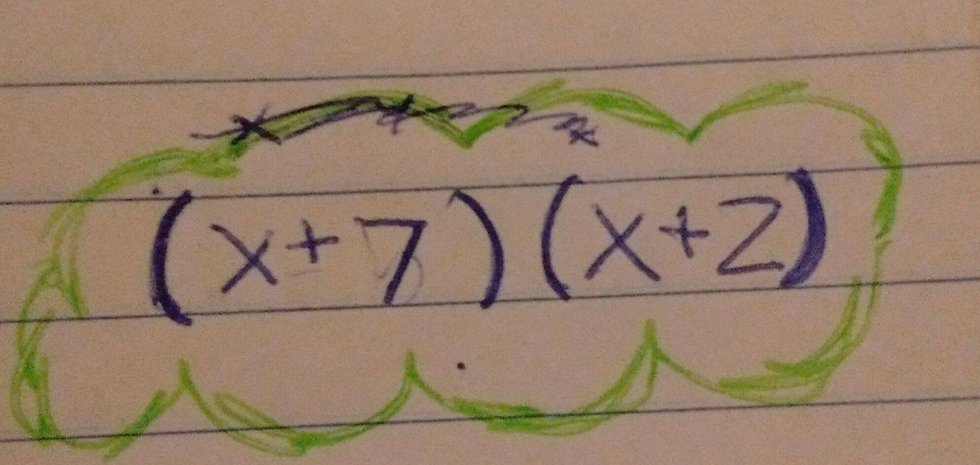

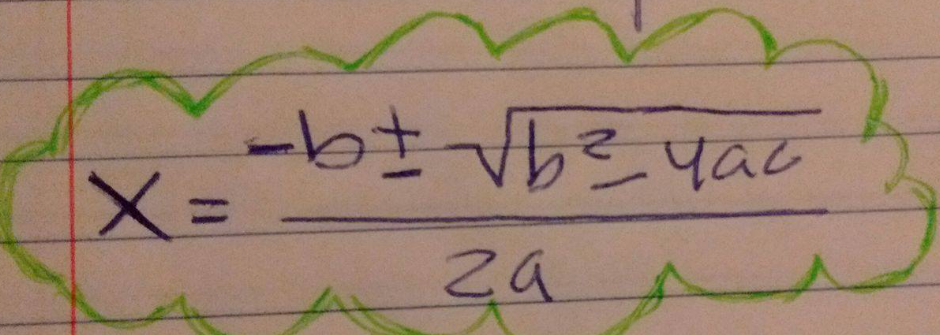

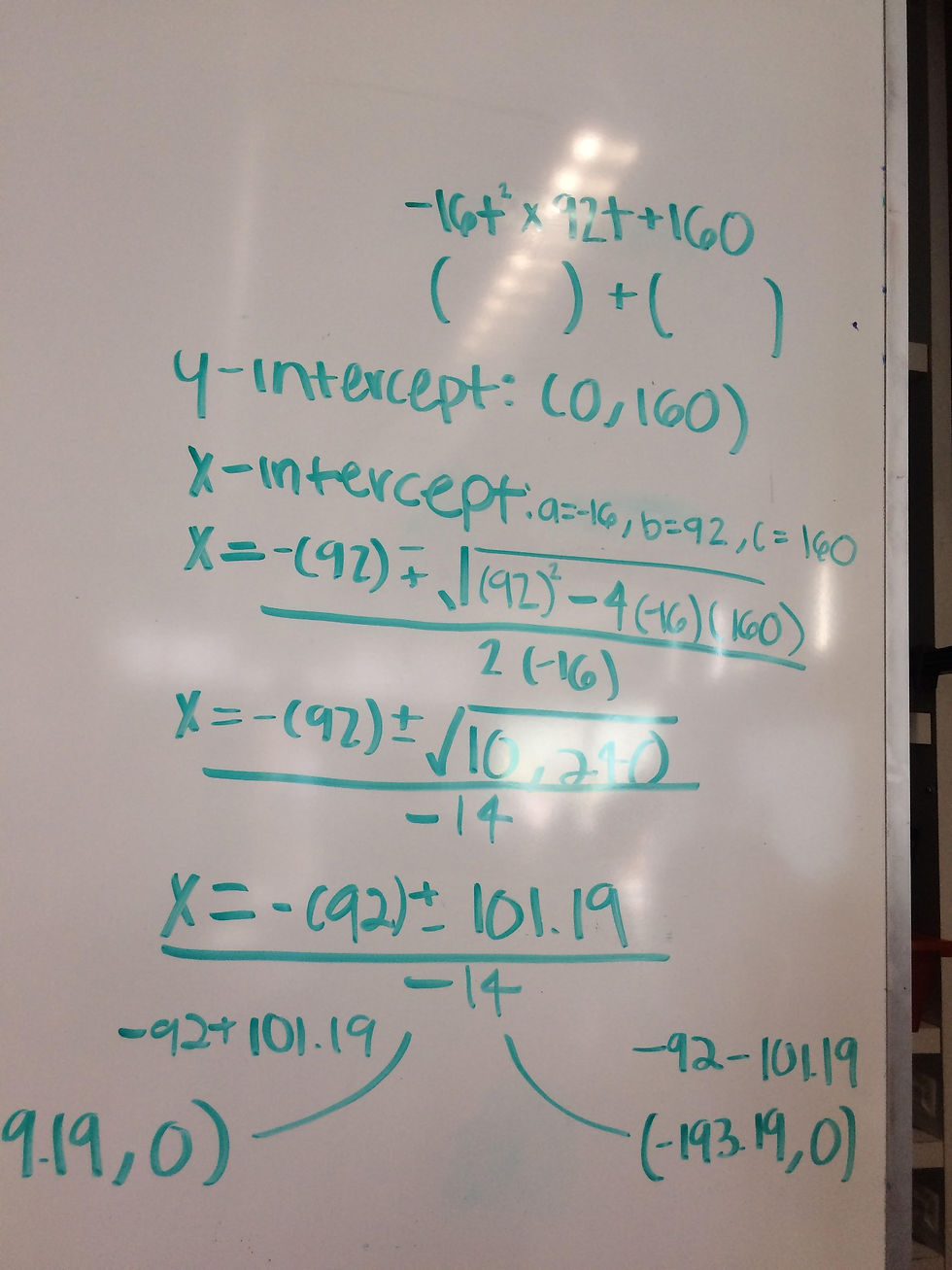
I failed this because I didn't solve for the 2(-16) And I some how changed it to -14
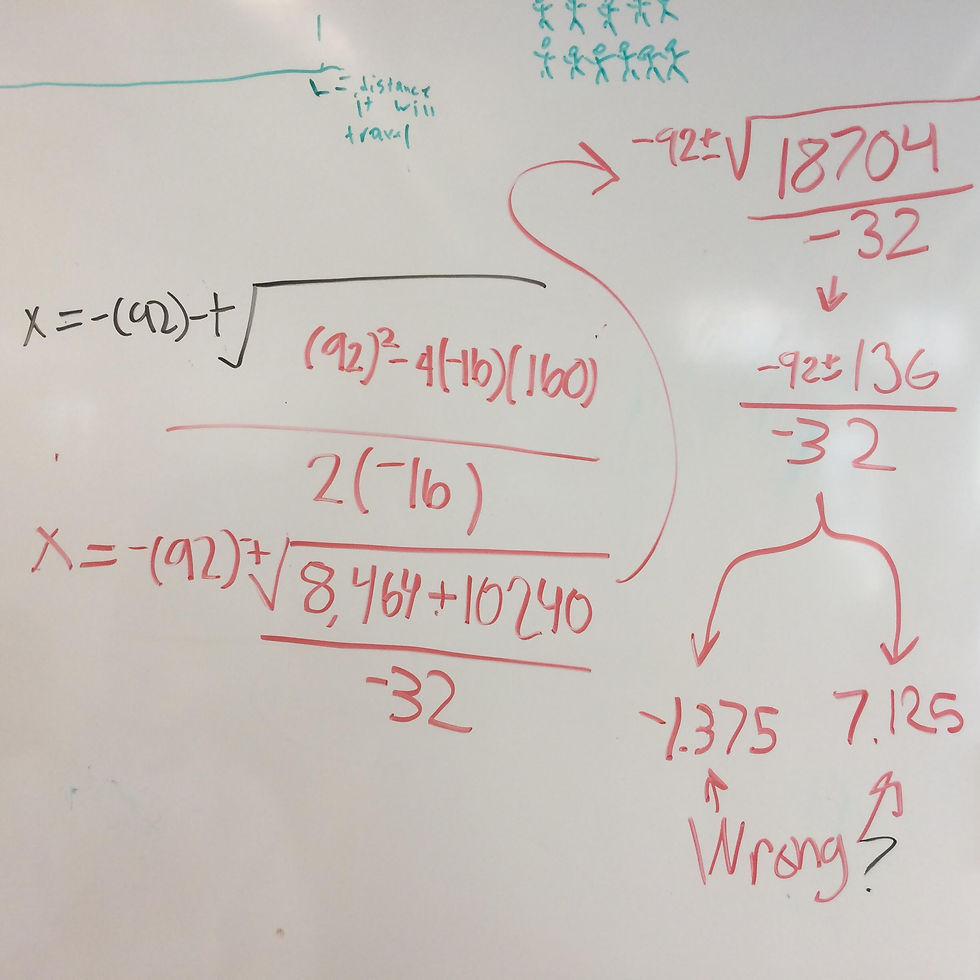
Thanks to my group mates they corrected that and got -32
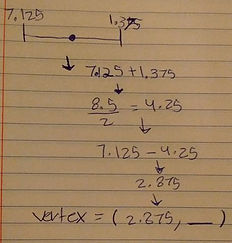
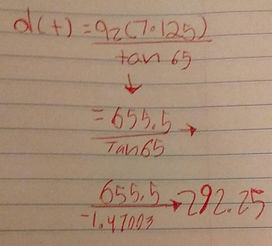
I'm a paragraph. Click here to add your own text and edit me. It's easy.