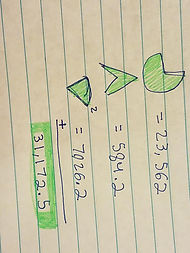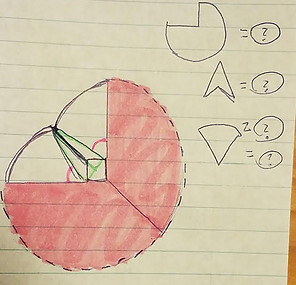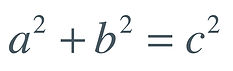LIDIA VAZQUEZ

Problem statement:

The cow problem: was presented to us with this information, there was a barn whom’s dimensions where 10x10 then there's is a cow tied to one of the edges of our barn our rope is hundred ft. therefore, we are trying to determine the area in which the cow has mobility to grow grass in that section only.

 

Process:

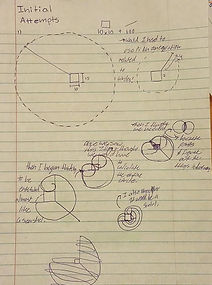
Once given the problem my initial attempt was to firstly visualize the problem. I began by drawing it out. I had many attempts my goal was to get the shape that was being created right. Because, it would be very unfortunate if I calculated everything for the wrong shape. I began with thinking that the circle revolved perfectly around the entire barn because the length of 100 ft sounded well. Until a classmate shared the point that if a rope is tied to a corner, every corner it would go around it would shorten. Once this thought was proposed I wondered whether it was shaped like a swirl almost like a seashell. After various contributions from classmates we reached the point where we had finally determined the shape. Which once seeing it,  the visual is looks pretty logical.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

 

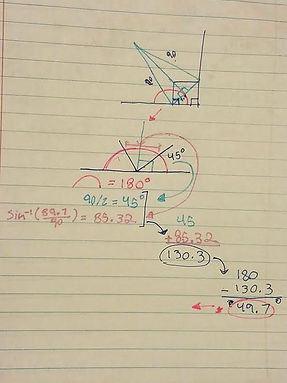
After we had the shape established. How could we began to calculate such an odd shape? I made a connection to previous math problems I had done where you would have to calculate the area by using other shapes to add up to the bizarre shape. But I had no clue where to began. We began to break the shape down we visualized the large ,pacman shaped, circle  and used the rope that represented it radius. Knowing this we used the formula Pi* R² . Then it was only a portion of a circle it was ¾ of a circle so we multiplied our answer by that. And received the area for that portion of  our shape.

 

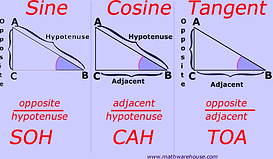
After that, we took a break from the problem and worked on learning the tools which would help us be able to solve the cow problem in the future. We learned about the pythagorean theorem and SOHCAHTOA

​

​

​

​

​

​

 

 

Image

 

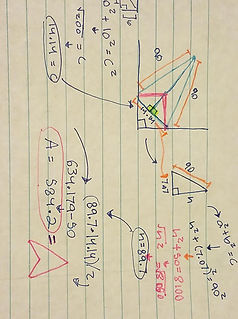
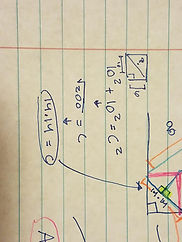
Once we were better equipped with mathematical tools such as the Pythagorean theorem and SOHCAHTOA. We were ready to tackle the cow problem again. Once having the circle section finished our main focus was centered on the funky shape that was being created in that quarter of the circle. In class a table groups we were encouraged to try to design different shapes that could be added to find the area. One of my group mates was able to get the right design which consisted of various triangles and two sectors. Since we had triangles to work with we began by solving the area of those. Since we connected the triangle to the “barn” or square we new what the dimension of the square, both sides were 10 yet we need to find the hypotenuse, so we used the pythagorean theorem.

 

 The answer was 14.14, and in our visual he had split those two triangles in half to create right triangles, therefore we did not know the height of those to find it we also had to use the pythagorean theorem. To calculate the height the find the area of the triangle which is base * Height. Giving us 634.2, after finding the area of all the triangles we had to subtract the overlapping area of the bar from the sum which gave us 584.2.

​

​

​

​

​

 

 

 

 

​
 

Now the only pieces that are left are the two sectors. Which are a bit more tricky personally for me. We began my identifying them as circles and then using a formula to find the percentage of the sector. To make it easier we visualized the sector just like the larger piece that we had done earlier the ¾  of the circle which was easy to identify, it was basically the same concept only not as easy to identify. We began by finding the radius since the rope shorten by ten ft when it wrapped around the barn the radius for our sectors was 90 which then we divided from 360 to receive a decimal. Then to be able to finish our sector calculations we had to identify the angles to find the angle of the sector. We began my noting that the first angle of the triangle was split from a 90 so it would give us 45 degrees. Then using inverse sine we were able to identify the second angle which was 85.32. We added them altogether and then subtracted 180 to find what you're missing angle was. It was 49.7 degrees using that information and the other gathered our final answer for the sectors was 7026.2.

 

​

 

​

​

​

Solution:

Finally we added all the parts together which gave us 31,172.5

 

To find this we used the pythagorean theorem, and SOHCAHTOA

 

 

 

 

 

 

 

 

 

​
 

Evaluation:

What I believe really push my thinking in the cow problem, was really gathering those mathematical tools then strategizing how to properly use them to solve this problem it was both challenging but super fun! Having developed an understanding of how to use this in different situations was very beneficial I think that what I got most out of was developing that skill of learning all the formulas and practicing on packets then applying it to complex or confusing problems. The group quiz affected me positively because, thanks to my group I was able to clarify somethings and I went to tutoring just to verify that I understood everything with the motive of understanding and not letting my team down.  If I were to grade myself I would give myself an A because I did put a lot of effort in this problem and understanding the different procedures I had actually never gone so much to tutoring I use going to tutoring as my resolutions each year in my pols yet this time I actually did go various times. And as a result I am proud of that and I am proud of my final understanding, and input.