LIDIA VAZQUEZ

Problem Statement:

The problem we were given was about how Mr. Tim was in need of the Flag Pole measurements, yet no one in school had them. Our goal was how to use a mathematical method to get an accurate calculation of what the Flag Pole’s height is.

 

Process Solution:

In order to find the best method possible we Tried 3 different methods to be able to achieve the most accurate answer. Throughout the month we have been working on different similarity theorems and when they can be applicable. When we were able to grasp all the theorems and how they work we moved on to trying different methods which we could use these rules to prove that they were equal, or proportionate.  

​

 Initial Guess:

 When we where faced with this problem the first strategy my group and I had was to measure through the unit of "Mr. Carter". We stacked mr. carters to have an approximate not very accurate calculation of how high the flagpole was . My groups initial guess was that it was 4 Mr. Carters.

​

Similarity: Is when a shape is equal to another one but its portions are larger. Similarly is when a shapes corresponding angles are equal to each other as well as the shapes corresponding lines are proportionate that they have a scale factor or a scale ratio.

 

Shadow Method:

With the shadow method, we knew that we needed first our height compared to the flagpoles, through our shadows. What my group and I did was we measured our heights and found an average height of a person and its shadow. Firstly we got a very dramatic calculation, pointing out that we had done something wrong we went back and redid it so that our numbers were more accurate. Since we were standing aligned with the flagpole therefore the sun was hitting the flagpole and the human at the same angle, and since the person is standing at a 90 angle as well as the pole the you had the AA theorem. We can use this theorem because once we position all these objects it creates two triangles, which we can prove their similar since we know those two triangles have two  corresponding angle that are equal to each other.

 

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

Mirror Method:

The mirror method was chosen because we had done other problems using it aswell, like the spider problem  which was a problem where we had to develop the high if we're all the spiders where , there was a mirror put in between the spiders and with the information of just ones length from the mirror as well as the height of another spider. The mirror method works because you have to  objects and a mirror in between them and those two objects are a certain length apart from this mirror calculating the length of the human or object and the flagpole from the mirror you have two length which you can find it ration and the mirror reflects a perfect angle and the person or flagpole have a 90 degree angle therefore you can use the theorem SAS. For the measurements we had 65  inches a sour input #1 then 29 inches as our input #2 and 135 inches as our input #3. Then since we knew where the had to out the measurements to cross multiply we plugged it in and solve for x which is equal to the height of the flagpole. 

 

​

​

​

​

​

 

​

​

​

​

​

​

Clinometer Method:

The clinometer method was the last method my group and I used. This method was dependent of the clinometer so that you calculate your eyesight and calculate your height and length away from the flagpole when you reach 45 degrees. Why is this important well because since we have created an isosceles triangle and we know that an isosceles triangle has two equal angles therefore, each angle would be a 45 degree angle. Seeing through the straw you either had to walk closer or farther away from the pole until you reached 45 degrees therefore mimicking the height of the flag pole.

​

​

​

​

​

​

​

​

​

​

​

​

 Final Calculation:

My groups final calculation was 25 ft. I believe that the most effective method of all was the last one the clinometer because it used the rule of the isosceles  triangle which I believe will hold more accuracy .

Problem Evaluation:

I really liked this problem because it was more challenging, due to the fact that not only did you have to do the math but a bg part of similarity s visualizing the problem an shapes, and proving whether it's true or not. My favorite part of this problem was when we had to prove a theorem through variables and transform the formula into another.The skill I learned to develop is that before solving use but justify or prove why they are similar, because it's a crucial point.

 

Self Evaluation:

If I would grade myself in this unit I would give myself an A , because I really worked hard every class and even if the problems were challenging You sure that I understood them. All my group in general was very engaged and we all worked well .

​

Edits-

Lorenzo-

Highlights- I like how specific it is, you used great vocabulary, I like how your problem evaluation

Critique-You have to specify the math part, explain what a clinometer is, add your opinion on the problem.

 

Zac-

Highlights-It’s very detailed, I like how you explain the different methods.

 

Ethan-

Highlights- very specific, explained methods well.

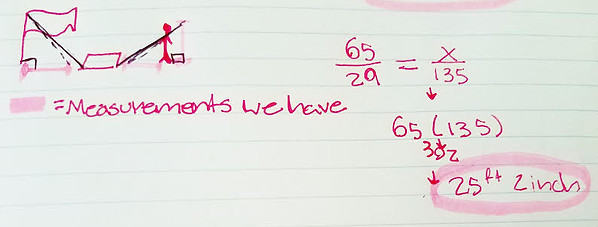
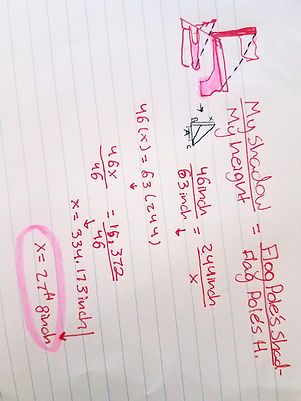
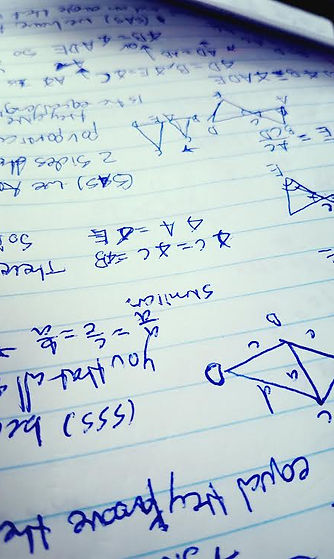
Critique- Maybe add pic, try giving an example of similarity.