PROBABILITY

Problem statement:

In this specific problem we are presented with three questions. The first question is how many number combinations are possible for a CA super Lotto ticket. The second question is , We now have to calculate the probability of winning the CA super lotto, we had been presented with this question before, but now that we have tackled probability this question, means more. The third question is now that we know the probability of winning , if you match all 6 numbers, you win $8,000,000. Another important point is that it cost $1 to play. With that are your expected winnings?

Now we were given these questions but there were certain rules or restrictions we had to follow. Which were there's six spots were we can place any numbers, in the first 5 spots we can only pick the numbers 1-47, and those numbers in that range of spots cannot repeat. The sixth spot is the mega number and the rules are different for that spot that number must be 1-27 and it may be repeated.

Process & Solution:

Our first initial guess was to look back

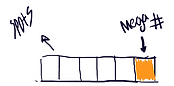
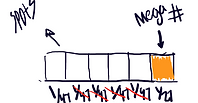
1) We began with the first problem, well “how many number combinations can you do?” We began to identify as a group the given and what we wanted to find out. Firstly, “what is our sample space?” we drew the spots that we had to fill out.

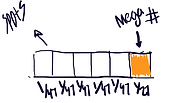
Then we went back to the rules or restrictions. Which were the first five spots had to 1-47. As a result of that Claudia said that we had to focus on each individual spot. So that's what we did we began to reason, “ alright so, if the first square is 1/27 why isn’t the next square exactly the same?” we went back to the gumball problem to specific problem that emphasis on the fact that if you are taking from your sample space and not reassembling or refilling it your sample space will reduce and if it is continues will it will continue to reduce more and more. revisiting this helped us answer this question of, “ if the first square is 1/27 why isn’t the next square exactly the same?”

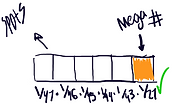
So know that we had established that the sample space would reduce since you couldn't repeat a number for those first five spots we wrote the probability for each spot.

Then my group and I needed to include the mega number and since we new there probability is 1/27 we just multiplied them altogether to get the answer.

2) Moving on to the second question, which was, “what is the probability of winning the CA Super Lotto?” Once we began to tackle the problem. I first stated to my group that the first thing we had to find was our sample space. Claudia explained to Arthur and I that our space would stay the same as the previous problem. I thought it had to be different because the other one was talking about all the combinations but I was able to understand why it stays the same. After that we were having difficulty in understanding what happened next. Ms. Ali came and hinted at us the next step. Thinking again of the 6 spots once you fill one spot down that's also decreasing your number on top. So that's what we did to better understand the concept.

3) Moving on to the third question which was, “if you match all 6 numbers, you win $8,000,000. Another important point is that it cost $1 to play, what are your expected winnings?” Firstly, I looked for my paper on expected value.

Seeing the formula I just had to plug in the Probability and the payouts, which my group and I had already acquired.

Site Title

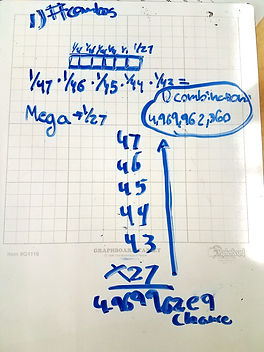
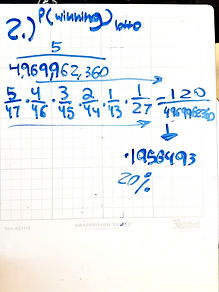
Problem Evaluation:

To be completely honest towards the beginning of probability, I was a little uneasy about my feelings towards probability, because it also had to do with reasoning about the word problem. But I loved the titanic problem and The super Lotto problem. I enjoyed it because once you reach that part where it makes it all flows so nicely. Also I think it's super cool how we can calculate the probability of winning the lottery and the fact that I don’t have to google it but I can actually figure it out, it’s the best! And Iike the structure that was similar to last semester, we are presented with the problem in the beginning of the unity, and then revisit once we have gathered enough skills to tackle it. When I am presented with that sort of structure I feel it’s the best, because I feel like mulan in that scene where she climbs the tree, and our golden tools are the math skills we have acquired. And I that's a feeling that should be crucial to have once you have solved a math problem because it shows that you have worked hard and have put a lot of effort understand it.

Self Evaluation:

If I were to grade myself in this unit I would give myself an A, because, I still worked hard and really enjoyed this unit. But I kind of stepped back this unit and allowed other classmates to explain, the problems. Which was really cool and it helped me to because they understood this unit better than I did. Overall I liked this unit a lot and It’s been even helpful in my philosophy class.

Edits:

Brianna-

Celebartions:

I liked what you were very specific

I liked that you were including people that helped you

Critical Feedback:

I think you should arrange the pictures differently

Make your title fonts more bold

And finish your self evaluation, and problem evaluation

Lorenzo-

I really love the layout of your DP really colorful, and really friendly. The images were eye catching with color never felt lost, and you did a great way of explaining the steps even for beginners really easy.

I think you should switch the A,B, and C to numbers, because it's more easy to follow. Also it looks more like steps, than having the letters it looks more like different steps for just 1 step.