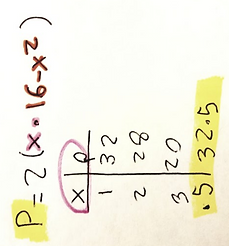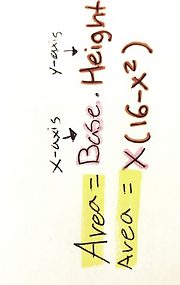LIDIA VAZQUEZ

Problem Statement:

The problem we were given had several restrictions but our over all objective was to find the perfect rectangle that could fulfill all the requirements and have the highest area. 

The first piece of information we where given was that a rectangle has one corner on the graph of y=16-x^2 and the other point is at 0 and the other one is in the positive axis the final point is in the function therefore the function is the boundary.

​

 

Process:

We began first by finishing the points to create the parabola with the function given.  We did this by listing out and plug in points into the function. Once we were able to get a clear understanding of where our parabola was. To focus on the next step of the problem that was to determine which triangle that fell into all the requirements could have the largest area. At first we drew some rectangles that we could create yet we noticed that there is truly an infinite number of triangles that could be created under those restrictions. So we chose an estimate of what the bigger triangle in whole numbers was. Then from there we began diving deeper into the numbers by incorporating decimals. We would do this by plugin them into the formula and trying to find a center where it gave you the largest number and then where the humber decreases as a reassurance that that's the highest number you can test. We were able to test numbers easily for the area by creating an equation that gave us the result we wanted we used to main equations.  One of them was A=x(16-x^2)  which calculated the area of the rectangle we formulated this by taking the fundamental  formula base times height is equal to the area of the base. And then put it in terms of the function given. Afterwards we selected different points to plug into the function and eliminated sections based on which numbers brought us closer to the highest  area. And then dove further into decimals. And then we did a similar procedure for the highest perimeter and used the formula h*2 + L*2 and then plugged numbers in that were consciously selected to test. And that's how we solved it.  

Solution:

The perimeter x =.5  The area  x= 2.31  

We came to this conclusion because this was the highest we could achieve. Of the final number we could have gone further into the decimals but we decided to keep it like that.  

 

Group Test:

My group prepared itself for the quiz by working on a similar problem a day before the test. The only problem is that one of our group mates was absent and we worked on the problem together but not truly worked collaboratively. We also worked on a very similar problem to the initial one we never thought of switching it up and incorporating the positive and negative side of the graph which could have been very beneficial for test day.  During test day my group and I worked really hard to understand the problem  we made sure that each group followed our pace which was a bit difficult since we had diverse ideas and thoughts on how to tackle the problem. Towards the end we were taking a lot of time do especially because we were over complicating the problem at the end we came to a solution and at least we all understood how to do the general theme of the problem.  I think our work was positive yet it could have been better in our overall communication and how to prepare together.  In the individual test we were firstly working very hurried because we finished our group test very late. I am not quite sure what happened I had the correct formula and concept but I didn’t plug it in correctly and that caused me to have the whole problem wrong. Also in the honors I understood how to plug in the function I had just forgotten that there was no need to modify it because it wasn't being doubled or mirrored anymore. Overall, in the individual test I know I grasped the concept there was just slight things that caused me to fail , therefore it was positive in a sense that I got to learn from my mistakes. The experience of this group quiz was alright I believe the most effective group quizzes are when you are with a group that you have worked with a little bit more to have a clear understanding of how they work together.

Evaluation/ Reflection:

I believe what really pushed my thinking was the fact that this was a concept I tend to struggle with which is more centered around lines and graphing. Therefore I went to tutoring and worked with Kandy and Dario on the problem. I also asked my group mates what they thought of and was able to be helped and to help as well as contribute once working with my group. I worked really hard on this quiz, the grade I think I should receive would be an B+ because I really did give it my best and afterwards I was able to understand the mistakes I had committed and I know that if I were to retake it I would have the concept down.